DEMATEL (Decision Making Trial and Evaluation) is a decision making technique based on pairwise comparisons. The DEMATEL method can be used to identify the model of causal relations between the variables. It shows causal relations and the factors’ exerted influences. The advantage of this method is that experts are able to be more fluent in expressing their opinions about the effects (direction and severity of effects) between factors.

The Steps of DEMATEL Method

Step 1: Generate the direct relation matrix

To identify the model of the relations among the n criteria, an n × n matrix is first generated. The effect of the element in each row is exerted on the element of each column of this matrix. If multiple experts' opinions are used, all experts must complete the matrix. arithmetic mean of all of the experts ' opinions is used and then a direct relation matrix X is generated.

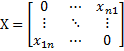
The following table shows the direct relation matrix, which is the same as pairwise comparison matrix of the experts.

Direct relation matrix

Step 2: Compute the normalized direct-relation matrix

To normalize, the sum of all rows and columns of the matrix is calculated directly. The largest number of the row and column sums can be represented by k. To normalize, it is necessary that each element of the direct-relation matrix is divided by k.

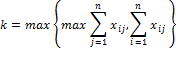
The normalized direct-relation matrix

Step 3: Compute the total relation matrix

After calculating the normalized matrix, the fuzzy total-relation matrix can be computed as follows:

In other words, an n × n identity matrix is first generated, then this identity matrix is subtracted from normalized matrix and the resulting matrix is reversed. The normalized matrix is multiplied by the resulting matrix to obtain the total relation matrix.

The total relation matrix

Step 4: set the threshold value

The threshold value must be obtained in order to calculate the internal relations matrix. Accordingly, partial relations are neglected and the network relationship map (NRM) is plotted. Only relations whose values in matrix T is greater than the threshold value are depicted in the NRM. To compute the threshold value for relations, it is sufficient to calculate the average values of the matrix T. After the threshold intensity is determined, all values in matrix T which are smaller than the threshold value are set to zero, that is, the causal relation mentioned above is not considered.

In this study, the threshold value is equal to 0.367

All the values in matrix T which are smaller than 0.367 are set to zero, that is, the causal relation mentioned above is not considered. The model of significant relations is presented in the following table.

The total- relationships matrix by considering the threshold value

Step 5: Final output and create a causal diagram

The next step is to find out the sum of each row and each column of T (in step 3). The sum of rows (D) and columns (R) can be calculated as follows:

Then, the values of D+R and D-R can be calculated by D and R, where D+R represent the degree of importance of factor i in the entire system and D-R represent net effects that factor i contributes to the system.

The table below shows the final output.

The final output

The following figure shows the model of significant relations. This model can be represented as a diagram in which the values of (D+R) are placed on the horizontal axis and the values of (D-R) on the vertical axis. The position and interaction of each factor with a point in the coordinates (D + R, D-R) are determined by coordinate system.

cause-effect diagram

Step 6: Interpret the results

According to the diagram and table above, each factor can be assessed based on the following aspects:

- Horizontal vector (D + R) represents the degree of importance between each factor plays in the entire system. In other words, (D + R) indicates both factor i’s impact on the whole system and other system factors’ impact on the factor. in terms of degree of importance, Innovation is ranked in first place and Crisis Management, Corporate Social\n Responsibility (CSR), Employee\n Satisfaction, Stakeholder\n Perception, Financial\n Performance, Industry Leadership, Product or Service\n Quality, Brand Image and Customer Satisfaction, are ranked in the next places.

- The vertical vector (D-R) represents the degree of a factor’s influence on system. In general, the positive value of D-R represents a causal variable, and the negative value of D-R represents an effect. In this study, Customer Satisfaction, Brand Image, Product or Service\n Quality, Industry Leadership, Stakeholder\n Perception are considered to be as a causal variable, Innovation, Corporate Social\n Responsibility (CSR), Financial\n Performance, Employee\n Satisfaction, Crisis Management are regarded as an effect.